

The last decades evolution of computational power, both in processing speed and memory size, has allowed a practical use of fundamental chemistry and physics in new materials and devices design. Brute force methods would require however powers which will probably be out of scope forever. Proper analysis of the objective and of the context, proper exploitation of available data and methods, carefully hand-crafted routines to save resources, are generally necessary to obtain useful results.
Multiple CPU, GPU and cloud computing does not tell the whole story. A standard job probably involves an ab-initio method (as for instance, some form of DFT), an adapted model (e.g. extended Hubbard), and the use of libraries and common tools which allow efficient treatment of structures and of dynamics. Acceptable results rest on the professional knowledge of all those involved.
Random materials response
We use basically two ways :Fast routines for sampling configurations : response is computed using standard methods for various configuration samples. The effectiveness is due to the efficiency of the code used (with proper simplification, directness and acceleration) and to the sampling of accessible configurations.
Stochastic routines, "according to Ghanem" : Roger Ghanem wrote in the '90 a practical implementation of finite element for stochastic materials. The considered variability is handled at once, at the price of a more involved preparation on the mathematical side. Implementation of this type of method have been described in public literature for various applications.
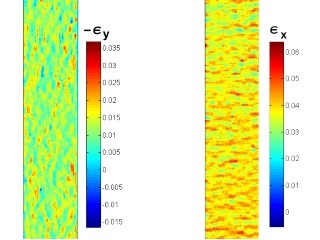
strain localization in tensile test
Breakdown phenomena and percolation
When transitions involve combinatorics, analytical solutions are often difficult to obtain, and computer simulations are required.
Formalism to study percolation and breakdown phenomena have been developed in the last decades, but successful applications and sensibility analysis require adapted representations of the context and of the target to be met.
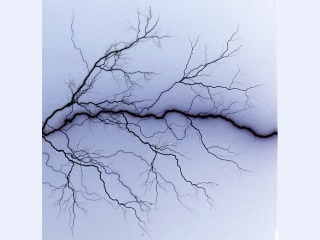
dielectric breakdown typical paths
Mean Field modeling
In some intractable problems, where required resources scale exponentially, chemists and physicists first proposed computational tricks leading to useful solutions (tricks often labeled as "metamagic" instead of mathematics).
One method allow to describe sufficiently precisely the difference between the searched solution and the solution of a reference well mastered problem which is close to the one to solve. A textbook example is the computation of the difference between an exponential integral and a gaussian integral, but the involved bookkeeping in original cases is made easier by computer algebra systems.

2d Ising problem as mean field example
Measurement and process analysis
Things often do not go the way we think they go, and we have to refrain to imagine what is happening.
Experimental work is valued by measurements with fast or slow data logging, on single or multiple channels. Nearly any acquisition can be done, eventually in collaboration with Universities or Service laboratories. Data can then be analyzed whatever the size and the format.

fast acquisition board
