

During the last decades, applied numerics, heuristics and algorithms took a larger place in chemicals and materials development.
Applied numerics allow to involve different professions within a common frame on a common target;
Heuristics allow to search and find an acceptable solution when the theory or our power would fall short of any result;
Algorithms can be polished on different cases and used on different fields.
Structural disorder
To explore materials properties, computational methods began with mono-crystalline materials and later, compositionally disordered materials.
Today work requires exploration of polycrystalline or amorphous materials, and of materials with various dopants and defects, and asks for a different and adapted approach.
The tools which have been developed and assembled in this application field are maturing and can be applied in various scene where irregularity precludes simpler methods.
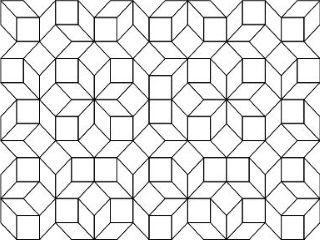
2d aperiodic tiling
Strong correlation
The need to deal properly with strong correlation has been for a long time a challenge in chemical problems as transition metal or rare-earth oxides properties (3d and 4f electrons).
After years, various industrial chemistry problems benefit from implemented and validated methods. Moreover those methods have been translated in other fields and implementation to deal with strong correlations outside chemistry are now effective (However one does not consider insurance or financial problems for which specific tools as copulas have been devised and are used).
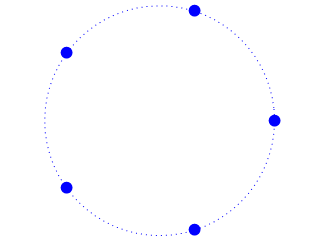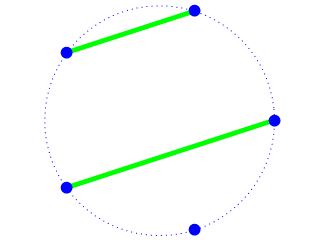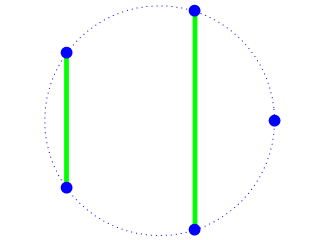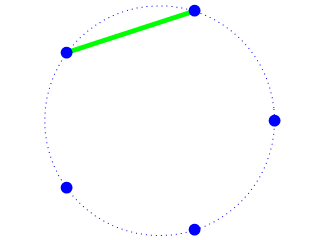
computation of Motzkin numbers
Contextual respect
An industrial problem to solve does not appear on a blank page, and many contextual constraints are to be considered for any useful work.
Data processing incorporate a definite and precise description of performance looked after, selection and parametrization of suitable production methods, availability and acceptability of materials. "Economic", "Green", "Durable", "Friendly" express many definite constraints which are an essential part of the problem to solve and have to be continuously considered.

common evaluation of problem constraints
